КАЗИНО
ДИСКЛЕЙМЕР
В данном проекте онлайн-казино рассматривается как мошенническая (scam) система, использующая азартные механики для манипуляции игроками. Работа носит учебно-исследовательский характер.
ОПИСАНИЕ ПРОЕКТА
Во время поиска датасетов для проекта я наткнулась на Kaggle на файл с результатами спинов онлайн-рулетки с мошеннического казино за 2023–2024 годы (https://www.kaggle.com/datasets/danielprezhernndez/fraudulent-european-roulette-dataset). Мне показалось интересным посмотреть, можно ли с помощью данных найти какие-то закономерности там, где игроки обычно их ожидают, и проверить, отличаются ли реальные цифры от ощущения «паттернов», которое часто возникает у людей при игре.
В данных зафиксированы выпавшие числа и цвета, что позволяет сравнивать реальные результаты игры с теоретической моделью классической рулетки.
Для проекта были использованы следующие типы визуализаций:
1. Кольцевая диаграмма
2. Гистограмма распределения
3. Линейный график накопленных отклонений
4. Линейчатая диаграмма с накоплением
Иллюстрации к теме проекта, отражающие зависимость от игры.
ЦВЕТОВАЯ ПАЛИТРА
При разработке цветовой схемы я стремилась подчеркнуть напряжённую атмосферу азартной игры и одновременно сохранить аналитическую строгость визуализаций. Основу палитры составляют контрастные тёмные оттенки, ассоциирующиеся с интерфейсами онлайн-казино, в сочетании с яркими акцентами, которые помогают выделять ключевые отклонения от нормы.
Для того, чтобы упорядочить цвета я использовала сервис Adobe Color (https://color.adobe.com/ru/).
В проекте применяются такие цвета: #1D1D1E #F9F7F5 #5E524B #78142C #C6953F #050505 #E9E3D6 #0B403A
Во всех элементах визуализации данных используется шрифт Manrope.
ГРАФИК 1
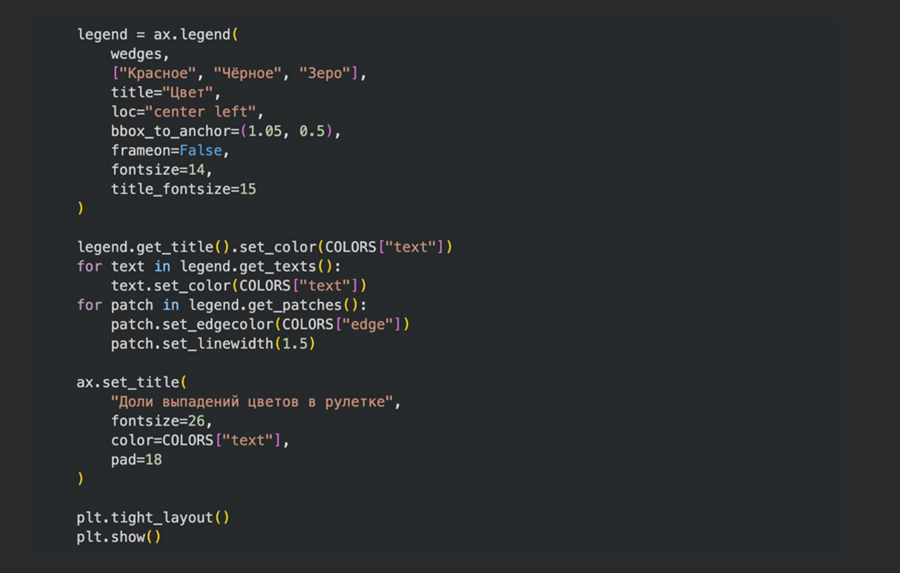
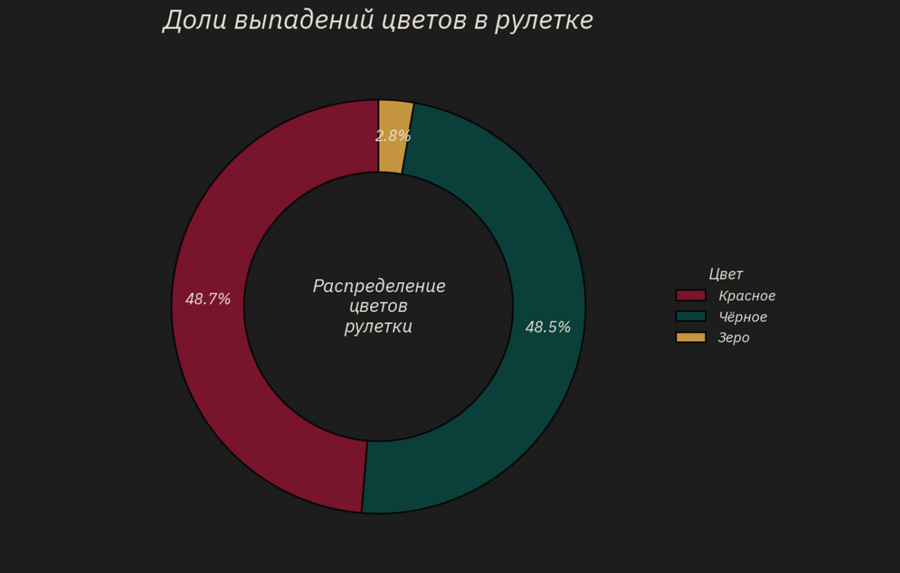
Первый этап анализа был посвящён сравнению частоты выпадения красного и чёрного цветов. Теоретически в европейской рулетке их вероятность практически одинакова, поэтому любое заметное смещение может вызывать подозрения у игроков.
С помощью диаграммы я сопоставила фактическое количество выпадений каждого цвета с ожидаемыми значениями, что позволяет сразу увидеть, есть ли перекос в распределении или различия укладываются в рамки статистической погрешности.
ГРАФИК 2
Далее я обратилась к анализу зеро — самого редкого, но психологически значимого элемента рулетки. Этот график показывает, как часто зеро появлялось по сравнению с теоретической вероятностью.
Отдельное внимание уделяется тому, что даже редкие события при большом количестве спинов начинают казаться «подозрительно частыми», хотя на самом деле могут оставаться в пределах нормы.
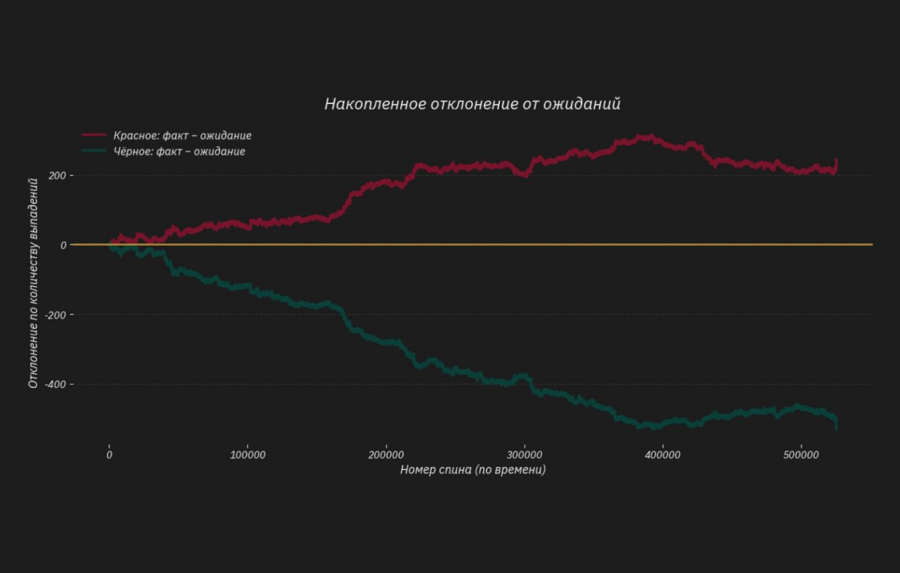
ГРАФИК 3
На этом графике показано, как реальные результаты рулетки отличаются от того, что мы ожидаем увидеть в теории. По горизонтали — время, то есть номер спина. По вертикали — накопленное отклонение от ожиданий. Если линия идёт вверх, значит этот цвет выпадал чаще, чем должен был. Если вниз — реже, чем ожидалось. Я хотела понять: «Если сравнить реальное количество выпадений красного и чёрного с тем, сколько их должно быть по теории, будут ли эти различия со временем исчезать или накапливаться?» Я знаю, что в рулетке:
вероятность красного ≈ 18/37
вероятность чёрного ≈ 18/37
То есть в среднем они должны выпадать одинаково часто. Я попросила ChatGPT помочь мне сформулировать расчёт.
Мой запрос был примерно такой:
«Помоги посчитать накопленное отклонение между фактическим количеством выпадений красного и ожидаемым количеством при заданной вероятности»
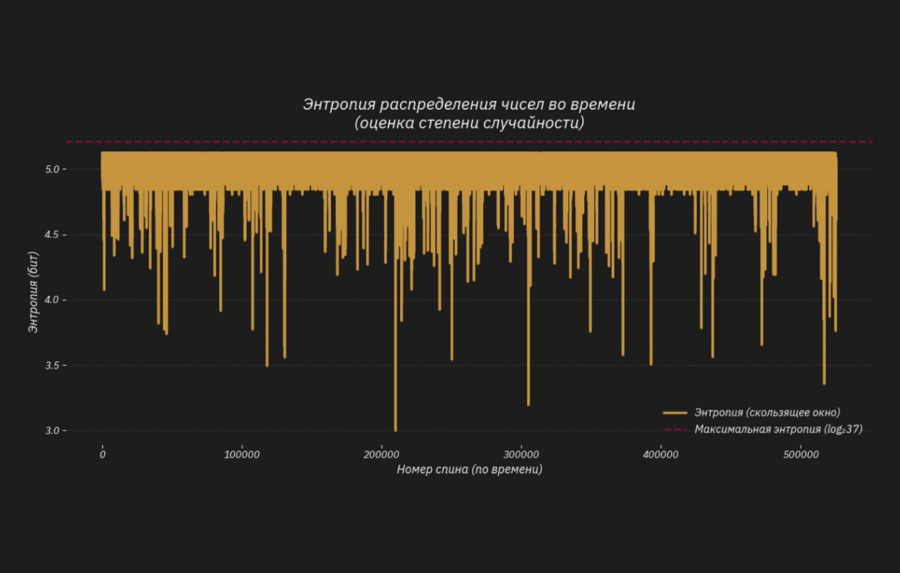
ГРАФИК 4
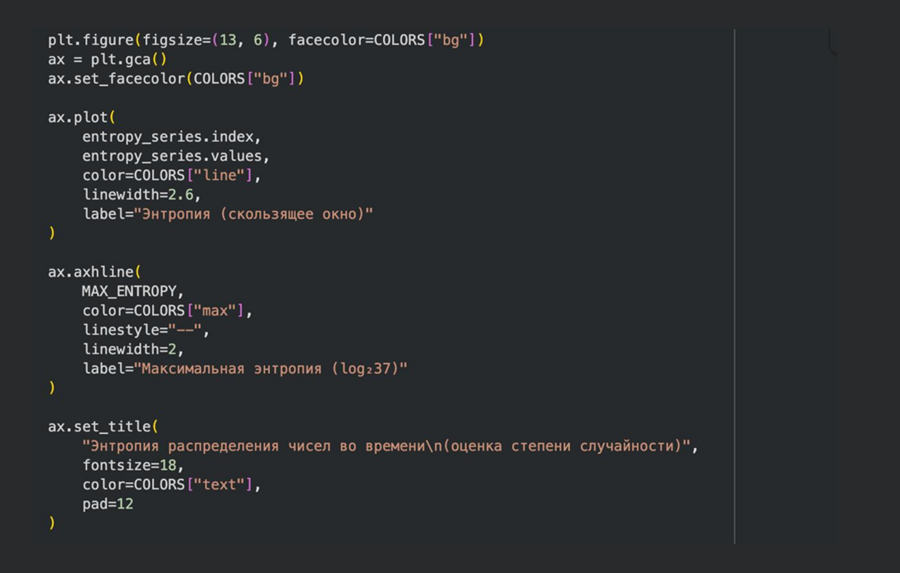
На графике «Стабильность случайности в рулетке» я показываю, насколько случайно ведёт себя рулетка со временем. Красная линия — это идеальный вариант, когда все числа выпадают максимально равномерно. Жёлтая линия — то, что происходит на самом деле. Она немного колеблется, и это нормально. Иногда кажется, что одни числа выпадают чаще, а другие реже, но это просто случайные колебания. Этот график показывает, что ощущение закономерностей возникает из-за того, как мы воспринимаем случайность, а не потому что система действительно меняется.
ЗАКЛЮЧЕНИЕ
Проведённый анализ показал, что данные мошеннической онлайн-рулетки в целом укладываются в рамки статистической случайности, несмотря на субъективное ощущение «нечестной игры». Распределение цветов и частота зеро не демонстрируют устойчивых отклонений, а выявленные колебания объясняются накопительным эффектом случайных событий. Графики ясно показывают, как человеческое восприятие стремится находить смысл и паттерны в шуме данных, особенно в условиях риска и эмоционального вовлечения. Визуальный анализ позволяет критически взглянуть на такие ощущения и заменить интуитивные выводы проверяемыми числовыми аргументами.
В итоге мой проект наглядно демонстрирует, что визуализация данных может служить эффективным инструментом для разоблачения мифов о «подстроенной» случайности и помогает лучше понять природу вероятностных процессов в цифровых системах.
Использованные статистические методы
В ходе анализа данных рулетки были применены методы описательной, вероятностной и разведочной статистики:
Частотный анализ категориальных данных — использовался для оценки распределения выпадений цветов рулетки (красное, чёрное, зеро). Подсчёт относительных частот позволил сравнить эмпирические доли цветов с теоретически ожидаемыми значениями для европейской рулетки.
Структурный анализ долей — реализован с помощью кольцевой диаграммы, что позволило наглядно отразить вклад каждого цвета в общее количество спинов и оценить симметрию распределения.
Анализ последовательностей и серий наблюдений — применялся для исследования длин серий спинов без выпадения зеро. Выделение непрерывных последовательностей между событиями позволило изучить поведение редких исходов.
Анализ распределения длин серий — выполнен через столбчатую диаграмму, что дало возможность оценить частоту коротких и длинных серий, а также выявить типичную длину серии между редкими событиями.
Оценка центральной тенденции для дискретного распределения — использовалась для расчёта среднего значения длины серии без зеро, которое было дополнительно визуально выделено на графике для интерпретации распределения.
Вероятностный анализ с использованием математического ожидания — применялся при сравнении фактического числа выпадений красного и чёрного цветов с их теоретически ожидаемыми значениями, рассчитанными на основе вероятностей европейской рулетки.
Анализ накопленных отклонений (cumulative deviation analysis) — реализован через вычисление разницы между наблюдаемыми и ожидаемыми значениями во времени. Такой подход позволил исследовать краткосрочные флуктуации и проверить отсутствие систематического смещения.
Анализ временных рядов — использовался для изучения динамики накопленных отклонений, что позволило визуально оценить характер колебаний вокруг нулевого уровня и подтвердить случайную природу процесса.
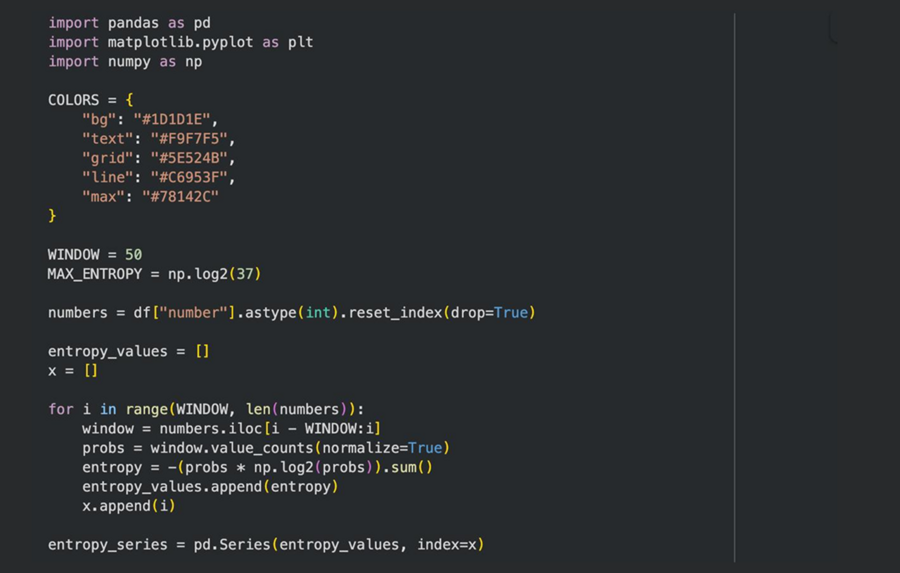
Энтропийный анализ — применялся для количественной оценки степени случайности последовательности выпавших чисел. Энтропия Шеннона рассчитывалась в скользящем временном окне, что позволило отслеживать изменения уровня неопределённости во времени.
Сравнение с теоретическим максимумом энтропии — использовалось для интерпретации результатов энтропийного анализа. Сопоставление эмпирической энтропии с максимальной возможной энтропией для равномерного распределения (log₂ 37) позволило оценить близость наблюдаемого процесса к идеальной случайности.
Описание применения генеративной модели и вспомогательных инструментов
1. Google Colab — Весь процесс работы: обработка данных и визуализация.
2. Kaggle — Платформа была использована для поиска и загрузки датасета.
3. Библиотеки Python kagglehub — для автоматического скачивания датасета matplotlib.font_manager — для подключения кастомного шрифта pandas — использовалась для загрузки датасета, очистки, преобразования и анализа табличных данных. matplotlib — основной инструмент для построения визуализаций в проекте. numpy — применялась для работы с числовыми данными и расчёта вспомогательных величин при построении графиков.
4. Цветовая палитра (Adobe Color)
5. ChatGPT — Нейросеть применялась для генерации и оптимизации кода, настройки визуального стиля графиков и корректировки функций анализа.
6. recraft.ai — Использовала для генерации обложки и иллюстраций.